ในบทความฉบับนี้จะกล่าวถึงสมการทางคณิตศาสตร์และการประยุกต์ใช้งานของตัวควบคุม PID รูปแบบขนาน (Parallel form) และรูปแบบมาตรฐาน (Standard form)
บทความฉบับนี้เป็นบทความที่ต่อเนื่องมาจากบทความเรื่อง ความรู้เบื้องต้นเกี่ยวกับตัวควบคุม PID
บทนำ
หากท่านได้เคยศึกษาหรือได้ใช้งานตัวควบคุม PID มาบ้างแล้ว บางท่านจะสังเกตเห็นได้ว่า รูปแบบสมการของตัวควบคุม PID นั้นมีมากกว่า 1 สมการ
แต่รูปแบบตัวควบคุม PID ที่พบเจอได้บ่อยและนิยมใช้งานกันมากมีอยู่ด้วยกัน 2 รูปแบบ คือ
- ตัวควบคุม PID รูปแบบขนาน (Parallel form PID Controller)
- ตัวควบคุม PID รูปแบบมาตรฐาน (Standard form PID Controller)
ตัวควบคุม PID รูปแบบขนาน (Parallel form PID Controller)
จากบทความเรื่อง ความรู้เบื้องต้นเกี่ยวกับตัวควบคุม PID ได้แสดงให้เห็นถึงรายละเอียดต่างๆ ของสมการตัวควบคุม PID
โดยมีสมการของตัวควบคุม PID คือ
![]()
ตัวควบคุม PID ที่ใช้สมการดังกล่าวจะถูกเรียกว่า “ตัวควบคุม PID รูปแบบขนาน”
โดยสมการของตัวควบคุม PID รูปแบบขนานนี้ในแต่ละพจน์ของ P, I และ D จะแยกออกจากกันเป็นอิสระ ไม่มีพารามิเตอร์ที่เกี่ยวพันธ์กัน ซึ่งการที่เป็นอิสระจากกัน จะทำให้ง่ายในการเขียนโปรแกรม ดังนั้นจึงนิยมนำสมการของตัวควบคุม PID รูปแบบขนานนี้มาใช้ในการเขียนโปรแกรมตัวควบคุม PID
เมื่อนำสมการของตัวควบคุม PID รูปแบบขนาน มาเขียนเป็นบล็อกไดอะแกรมควบคุม จะได้ดังรูปที่ 1
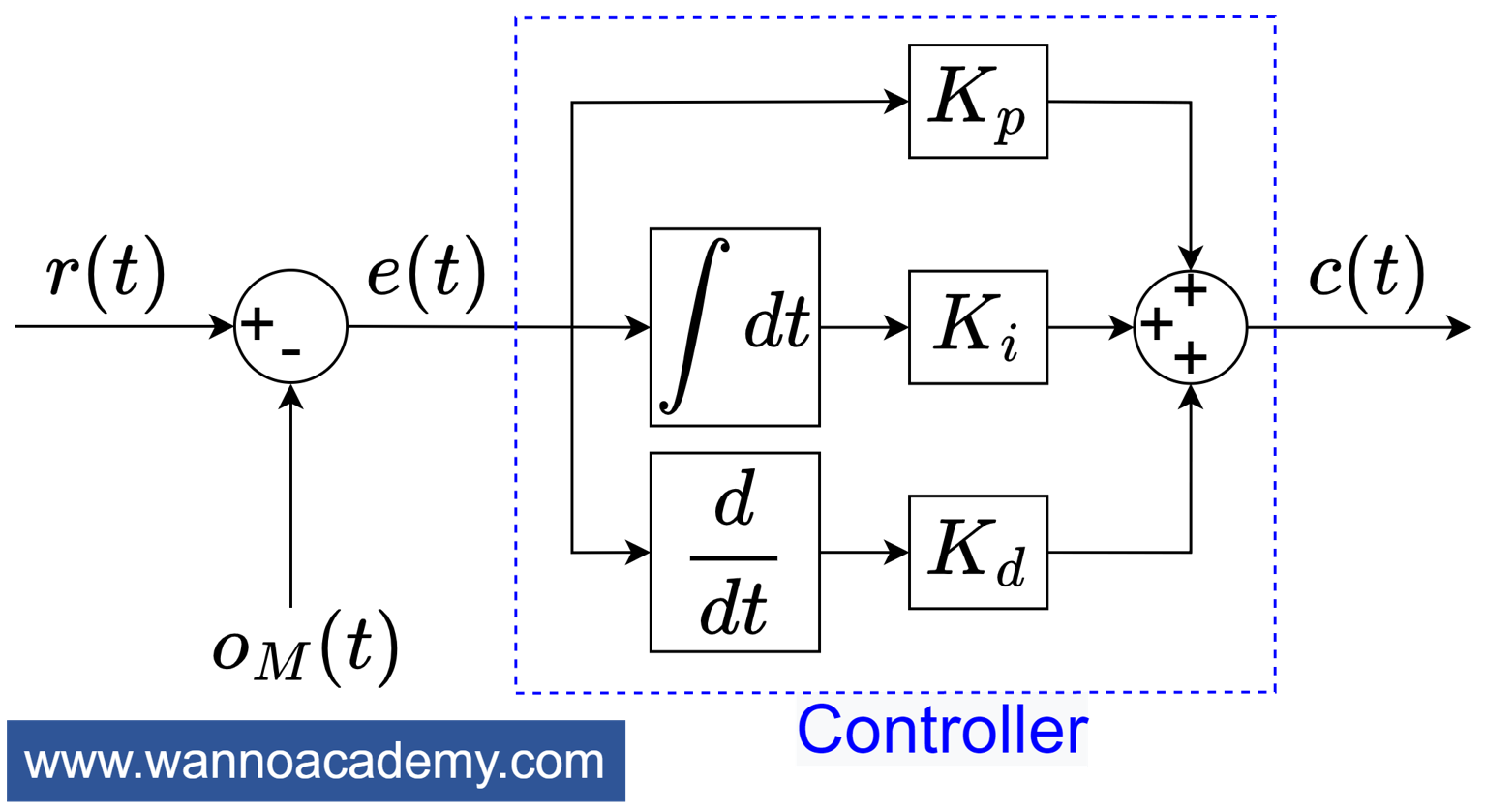
ตัวควบคุม PID รูปแบบมาตรฐาน (Standard form PID Controller)
รูปแบบตัวควบคุม PID อีกรูปแบบหนึ่งที่นิยมใช้กันอย่างแพร่หลายและเป็นรูปแบบที่ถูกใช้ในการหาพารามิเตอร์ของตัวควบคุม PID ด้วยวิธีต่างๆอย่างมากมายนั้นคือ “ตัวควบคุม PID รูปแบบมาตรฐาน”
ซึ่งมีสมการดังนี้คือ
![]()
โดยที่
![]() คือ อัตราขยายสัดส่วน (Proportional gain)
คือ อัตราขยายสัดส่วน (Proportional gain)
![]() คือ เวลาปริพันธ์ (Integral time)
คือ เวลาปริพันธ์ (Integral time)
![]() คือ เวลาอนุพันธ์ (Derivative time)
คือ เวลาอนุพันธ์ (Derivative time)
สมการรูปแบบขนานนี้พจน์ในแต่ละพจน์ P, I และ D จะไม่แยกออกจากกันเป็นอิสระ แต่จะมีพารามิเตอร์ที่เกี่ยวพันธ์กับทุกพจน์คือ ![]()
ตัวควบคุม PID รูปแบบมาตรฐานนี้จะเหมาะกับการจูนตัวควบคุม PID
เพราะจะมีบางครั้งที่ต้องเพิ่มหรือลดอัตราขยายของทั้ง 3 พจน์พร้อมๆ กัน ซึ่งสามารถทำได้โดยจูนค่า ![]() เพียงแค่ค่าเดียว
เพียงแค่ค่าเดียว
ซึ่งจะต่างจากรูปแบบขนานซึ่งจะต้องจูนทั้ง 3 ค่าในเวลาเดียวกันซึ่งก่อให้เกิดความไม่สะดวกในการจูนค่า และโดยส่วนใหญ่การหาพารามิเตอร์ของตัวควบคุม PID ไม่ว่าจะเป็นวิธีของ Ziegler-Nichols หรือวิธีของ Chien-Hrones-Reswick เป็นต้น ก็จะอยู่บนพื้นฐานตัวควบคุม PID รูปแบบมาตรฐาน
เมื่อนำสมการของตัวควบคุม PID รูปแบบมาตรฐาน มาเขียนเป็นบล็อกไดอะแกรมควบคุม จะได้ดังรูปที่ 2
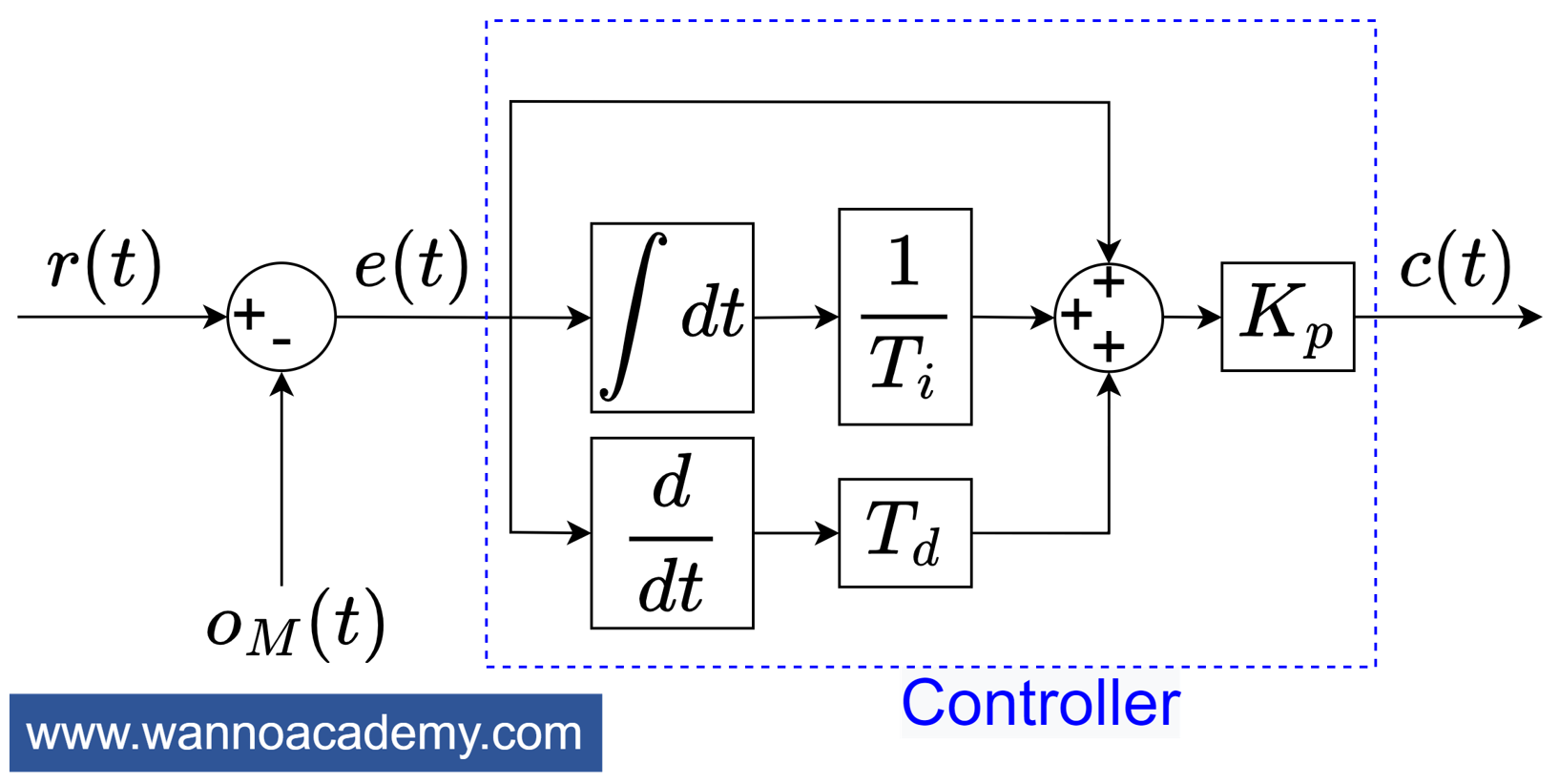
สัมพันธ์ระหว่างตัวควบคุม PID รูปแบบขนานกับตัวควบคุม PID รูปแบบมาตรฐาน
ในบางครั้งอาจมีความจำเป็นต้องมีการแปลงพารามิเตอร์ระหว่างตัวควบคุม PID รูปแบบขนานและตัวควบคุม PID รูปแบบมาตรฐานไปมาระหว่างกัน
เพื่อหาความสัมพันธ์ระหว่างตัวควบคุม PID รูปแบบขนานกับตัวควบคุม PID รูปแบบมาตรฐาน สามารถทำได้ดังนี้
นำ ![]() ของรูปแบบมาตรฐานคูณกระจายเข้าไปในวงเล็บจะได้
ของรูปแบบมาตรฐานคูณกระจายเข้าไปในวงเล็บจะได้
![]()
เทียบสัมประสิทธิ์สมการนี้กับสมการรูปแบบขนานจะได้
![]()
![]()
![]()
ซึ่งความสัมพันธ์นี้จะถูกใช้และมีประโยชน์มากในการหาอัตราขยายตัวควบคุม PID ซึ่งจะได้กล่าวในบทความถัดไป
ข้อมูลเพิ่มเติม
- เนื้อหาของบางส่วนของบทความฉบับนี้เป็นส่วนหนึ่งของ คอร์สตัวควบคุม PID ขั้นพื้นฐาน
หากท่านมีคำถามหรือข้อสงสัยประการใดสามารถสอบถามได้ที่
(เมื่อเข้า Wanno Acedemy ได้แล้ว กดส่งข้อความ เพื่อเริ่มพูดคุยกับผมได้เลยครับ)
