ความรู้เบื้องต้นเกี่ยวกับตัวควบคุม PID Wanno Academy

บทความฉบับนี้เป็นบทความเกี่ยวกับความรู้เบื้องต้นของตัวควบคุม PID ซึ่งประกอบไปด้วย สมการคณิตศาสตร์ของตัวควบคุม PID, บล็อคไดอะแกรมตัวควบคุม PID, การกระทำทางคณิตศาสตร์ของตัวควบคุม PID และผลต่อตัวแปรเอาต์พุตของระบบ

บทความฉบับนี้เป็นบทความที่ต่อเนื่องมาจากบทความเรื่อง Open-loop Control System vs Closed-loop Control System

จากบทความเรื่องระบบควบคุมแบบวงเปิดและระบบควบคุมแบบวงปิด จะเห็นได้ว่าตัวควบคุม PID มีสมรรถนะที่ดีกว่ามากเมื่อเทียบกับระบบควบคุมแบบวงเปิดในการกำจัดสิ่งรบกวนออกไปจากระบบควบคุม

ดังนั้นในบทความฉบับนี้จะมาเรียนรู้กันว่าตัวควบคุม PID คืออะไรและมันทำงานอย่างไร

ตัวควบคุม PID คืออะไร

ตัวควบคุม PID คือตัวควบคุมชนิดหนึ่งที่ใช้ในการควบคุมระบบในระบบควบคุมแบบวงปิด ซึ่งสามารถทำให้ระบบที่กำลังถูกควบคุมมีสมรรถนะที่ดีขึ้นมาได้ทั้งในด้านความเร็ว ความถูกต้องแม่นยำและในทางเสถียรภาพ

Closed-loop control block diagram — รูปที่ 1

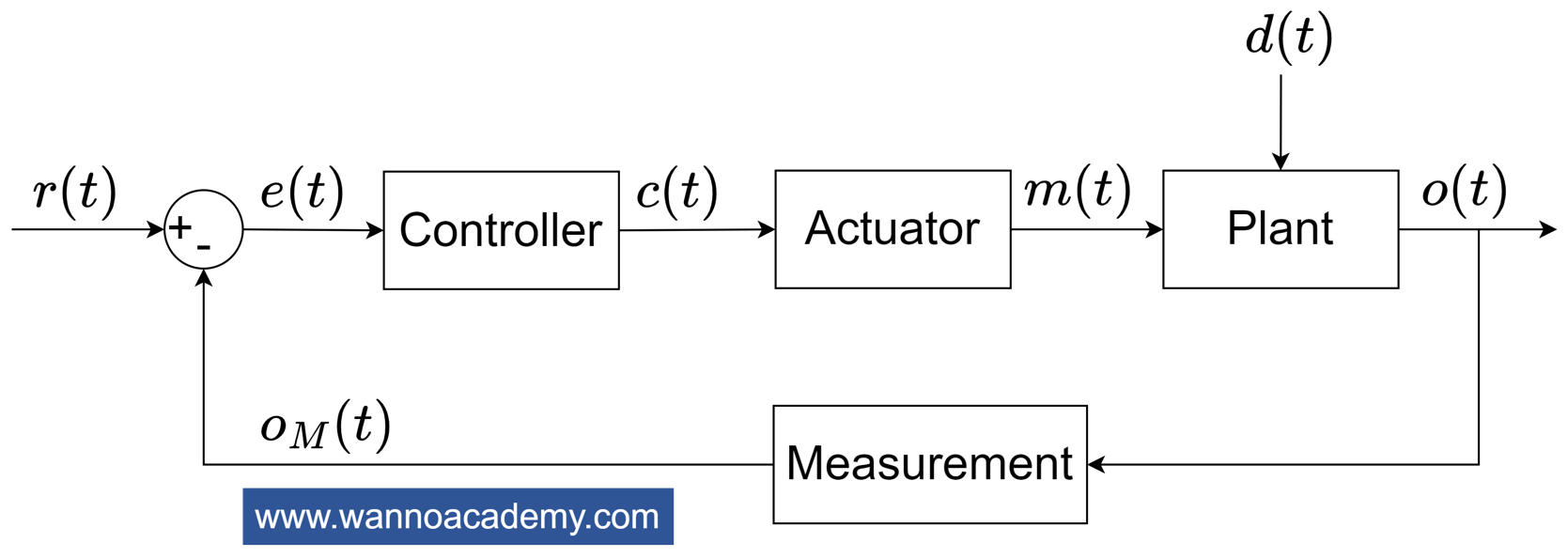
รูปที่ 1 เป็นบล็อกไดอะแกรมระบบควบคุมแบบวงปิด ซึ่งตัวควบคุมในระบบควบคุมแบบวงปิดที่นิยมใช้กันมากไม่ว่าจะเป็นในวงการนักประดิษฐ์ งานวิจัยหรือในภาคอุตสาหกรรม นั้นคือ ตัวควบคุม PID

PID ย่อมาจากคำว่า Proportional-Integral-Derivative

Proportional (P) คือ สัดส่วน

Integral(I) คือ ปริพันธ์

Derivative (D) คือ อนุพันธ์

สมการของตัวควบคุม PID

สมการทางคณิตศาสตร์ของตัวควบคุม PID มีดังต่อไปนี้

ตัวควบคุม P

มีสมการคือ

$c_P(t)=K_pe(t)$

โดยที่

$c_P(t)$ คือ ตัวแปรควบคุมของ P

$K_p$ คือ อัตราขยายสัดส่วน (Proportional gain)

$e(t)$ คือ ตัวแปรความผิดพลาด ซึ่งสามารถหาได้จาก

$e(t)=r(t)-o_M(t)$

โดยที่

$r(t)$ คือ ตัวแปรอ้างอิง

$o_M(t)$ คือ ตัวแปรเอาต์พุตที่ได้จากการวัด

ตัวควบคุม I

มีสมการคือ

$c_I(t)=K_i\int{e(t)d(t)}$

โดยที่

$c_I(t)$ คือ ตัวแปรควบคุมของ I

$K_i(t)$ คือ อัตราขยายปริพันธ์ (Integral gain)

ตัวควบคุม D

มีสมการคือ

$c_D(t)={K_d\frac{de(t)}{dt}}$

โดยที่

$c_D(t)$ คือ ตัวแปรควบคุมของ D

$K_d(t)$ คือ อัตราขยายอนุพันธ์ (Derivative gain)

ตัวควบคุม PID

คือนำสมการของตัวควบคุมทั้ง 3 สมการมารวมกัน ได้สมการดังนี้คือ

$c(t)=c_P(t)+c_I(t)+c_D(t)$

$c(t)={K_pe(t)+K_i\int{e(t)d(t)}+K_d\frac{de(t)}{dt}}$

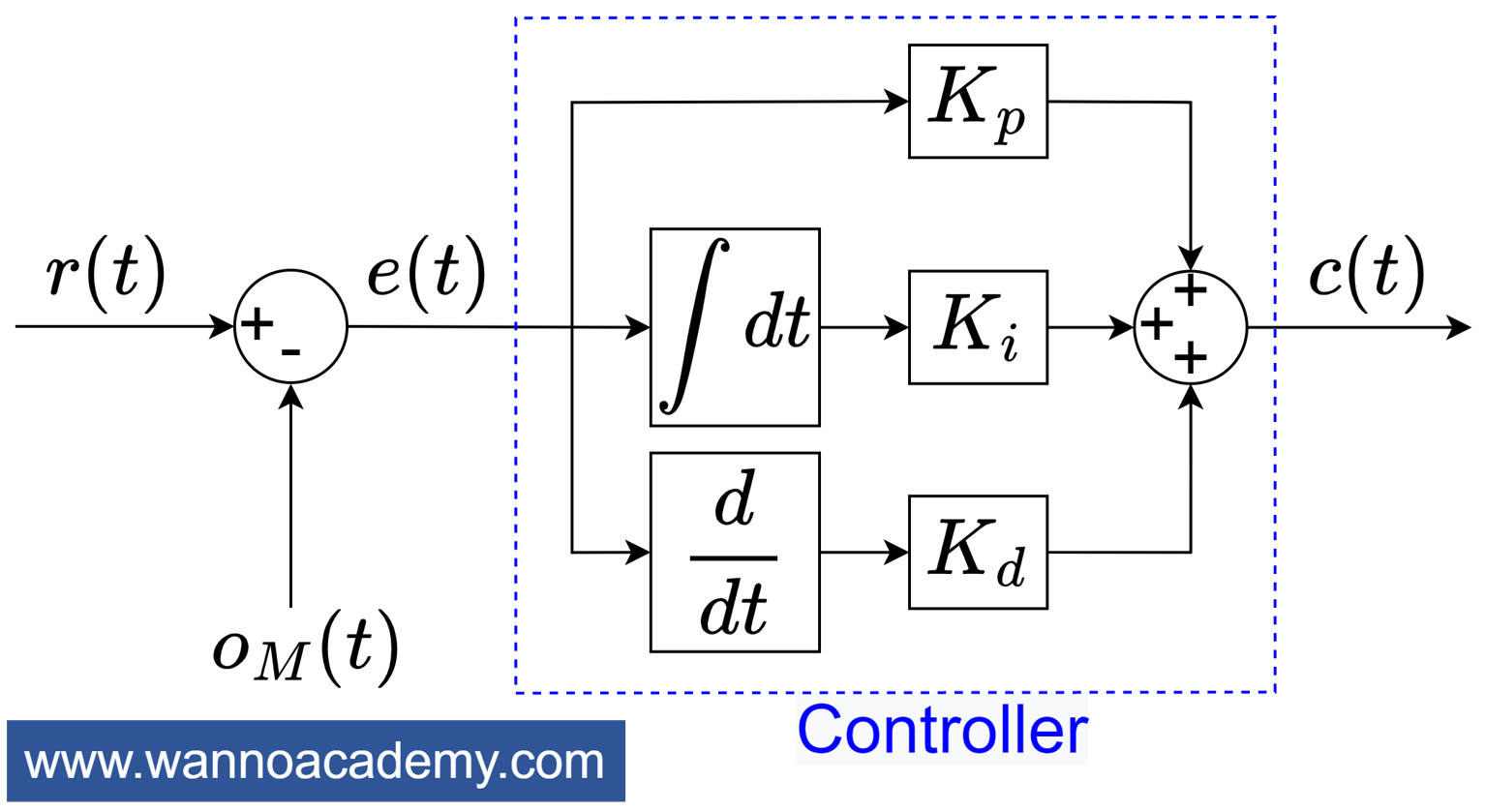
บล็อกไดอะแกรมตัวควบคุม PID

เมื่อนำสมการของตัวควบคุม PID มาเขียนเป็นบล็อกไดอะแกรมควบคุม จะได้ดังรูปที่ 2

การกระทำทางคณิตศาสตร์ของตัวควบคุม PID และผลต่อตัวแปรเอาต์พุตของระบบ

จากสมการทางคณิตศาสตร์ของตัวควบคุม PID สามารถอธิบายลักษณะการกระทำทางคณิตศาสตร์ของตัวควบคุม PID และผลต่อตัวแปรเอาต์พุตของระบบ ได้ดังตารางที่ 1

ตารางที่ 1

	การกระทำทางคณิตศาสตร์	ผลต่อตัวแปรเอาต์พุต
P	เป็นสัดส่วนโดยตรงกับตัวแปรความผิดพลาด	เพิ่มหรือลดความเร็ว
I	เป็นการหาพื้นที่ใต้กราฟของตัวแปรความผิดพลาด	ลดค่าความผิดพลาด
D	เป็นการหาความชันของตัวแปรความผิดพลาด	ลดการแกว่งและการพุ่งเกิน

ข้อมูลเพิ่มเติม

เนื้อหาบางส่วนของบทความฉบับนี้เป็นส่วนหนึ่งของ คอร์สตัวควบคุม PID ขั้นพื้นฐาน

หากท่านมีคำถามหรือข้อสงสัยประการใดสามารถสอบถามได้ที่

Facebook: Wanno Academy

(เมื่อเข้า Wanno Acedemy ได้แล้ว กดส่งข้อความ เพื่อเริ่มพูดคุยกับผมได้เลยครับ)