เส้นโค้งปฏิกิริยา (Reaction curve) คือ กราฟผลตอบสนองตัวแปรเอาต์พุตของระบบวงเปิดเมื่อป้อนอินพุตให้กับระบบเป็นฟังก์ชันขั้นบันได
เส้นโค้งปฏิกิริยา (Reaction curve) คืออะไร
เส้นโค้งปฏิกิริยา (Reaction curve) คือ กราฟผลตอบสนองตัวแปรเอาต์พุตของระบบวงเปิดเมื่อป้อนอินพุตให้กับระบบเป็นฟังก์ชันขั้นบันได
โดยมีบล็อกไดอะแกรมในการทดสอบระบบเพื่อหาเส้นโค้งปฏิกิริยาดังรูปที่ 1
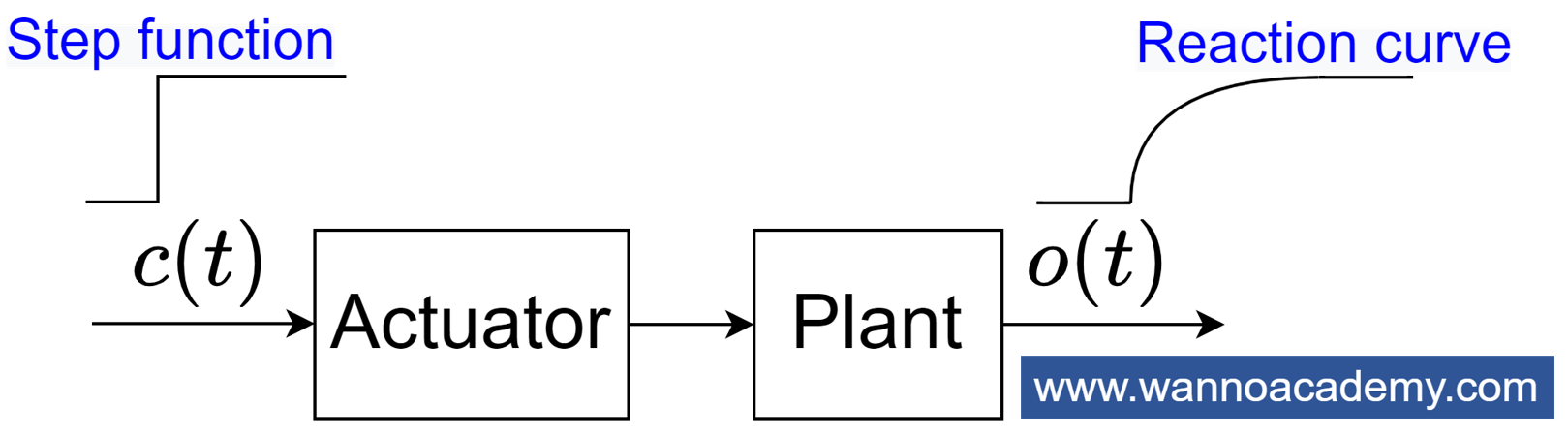
ประโยชน์ของเส้นโค้งปฏิกิริยา
ทำให้รู้ข้อมูลเบื้องต้นเกี่ยวกับระบบที่กำลังจะควบคุม ว่าก่อนการควบคุมระบบมีลักษณะอย่างไร ได้แก่
- เป็นระบบที่มีผลตอบสนองช้าหรือเร็ว
- มีสัญญาณรบกวนในระบบมากน้อยเพียงใด
- ผลตอบสนองของระบบมีเวลาประวิง (delay time systems) หรือไม่มีเวลาประวิง (non-delay time systems)
สามารถนำไปหาอัตราขยายของตัวควบคุม PID
ขั้นตอนในการหาพารามิเตอร์ของเส้นโค้งปฏิกิริยา
ตัวอย่างที่แสดง เป็นการหาเส้นโค้งปฏิกิริยาของระบบควบคุมแรงดันเอาต์พุตของวงจร RC
ขั้นตอนในการหาเส้นโค้งปฏิกิริยาดังต่อไปนี้
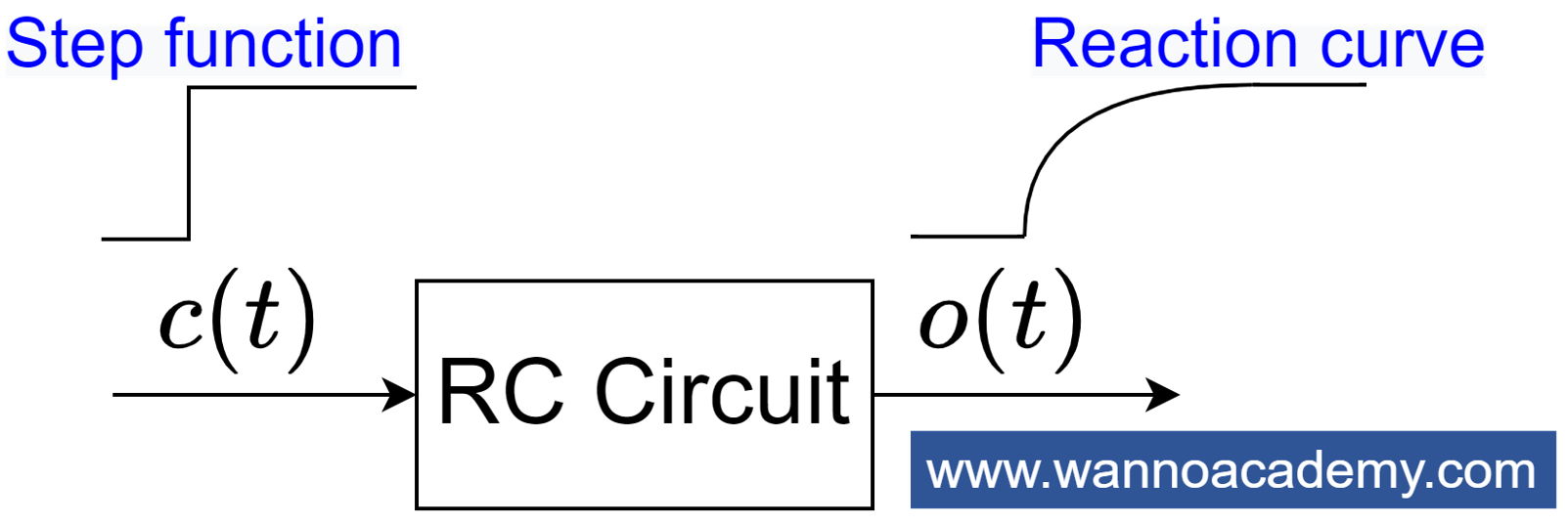
1. จ่ายสัญญาณอินพุตคือตัวแปรควบคุม ![]() ซึ่งเป็นฟังก์ชันขั้นบันไดเข้าสู่ระบบ ดังรูปที่ 2 พร้อมทั้งบันทึกค่าตัวแปรควบคุม
ซึ่งเป็นฟังก์ชันขั้นบันไดเข้าสู่ระบบ ดังรูปที่ 2 พร้อมทั้งบันทึกค่าตัวแปรควบคุม ![]() และตัวแปรเอาต์พุต
และตัวแปรเอาต์พุต ![]() เพื่อนำไปพล็อตกราฟ
เพื่อนำไปพล็อตกราฟ
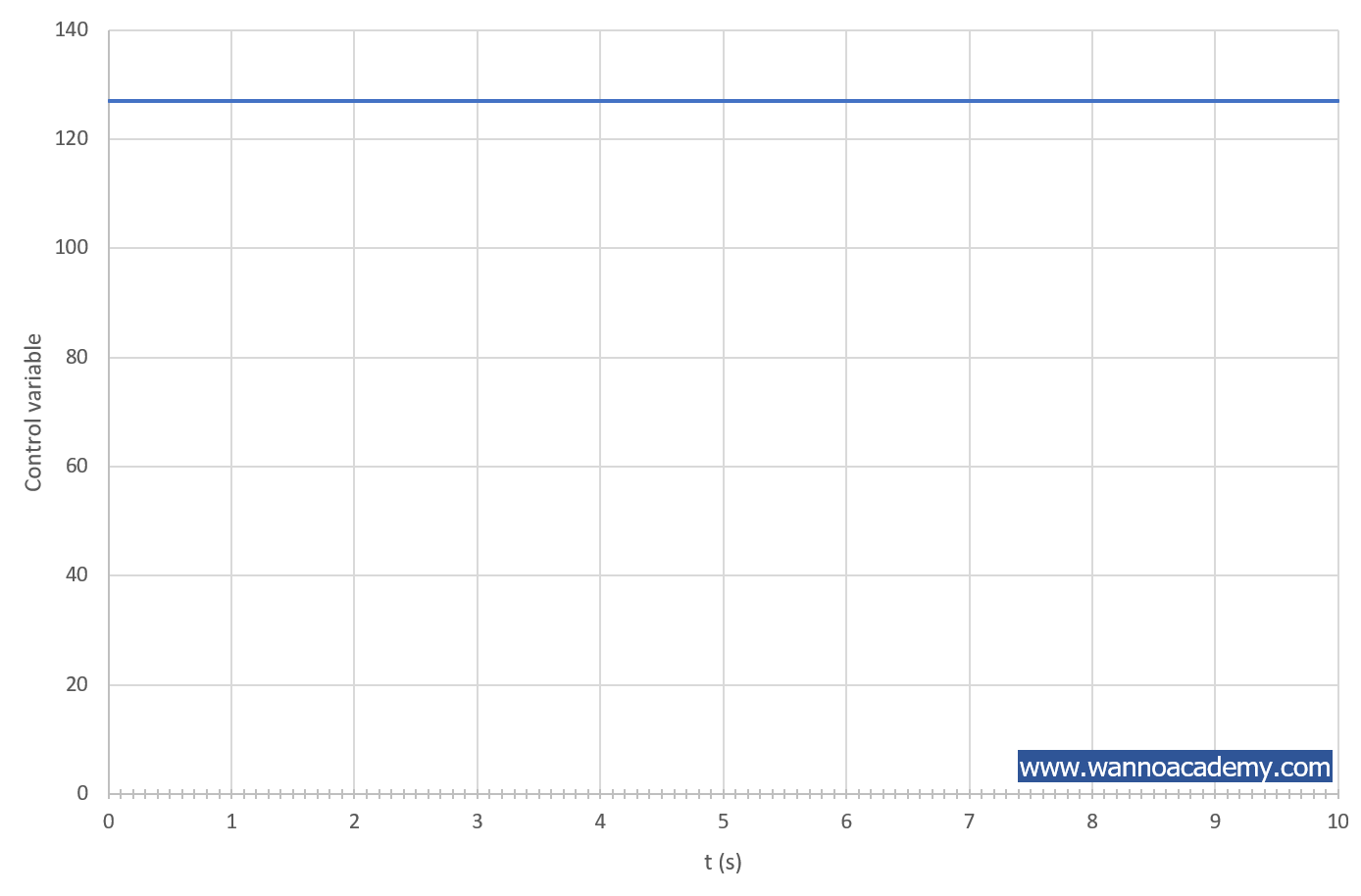
2. พล็อตกราฟอินพุตซึ่งคือตัวแปรควบคุม ![]() ดังรูปที่ 3 และเส้นโค้งปฏิกิริยาของตัวแปรเอาต์พุต
ดังรูปที่ 3 และเส้นโค้งปฏิกิริยาของตัวแปรเอาต์พุต ![]() ดังรูปที่ 4
ดังรูปที่ 4
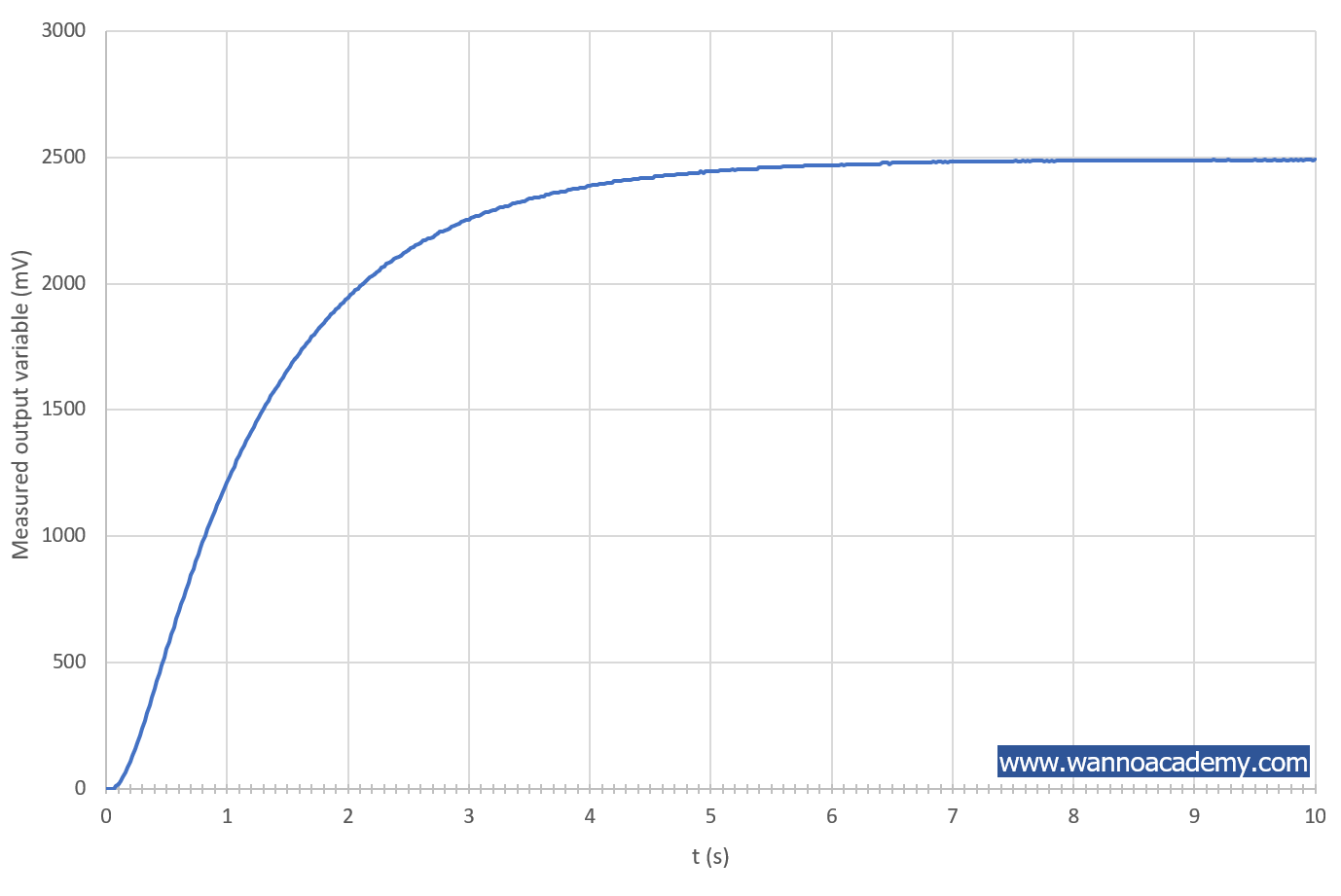
3. ทำการลากเส้นตัดกราฟเพื่อหาพารามิเตอร์ของกราฟอินพุตฟังก์ชันขั้นบันไดดังรูปที่ 5
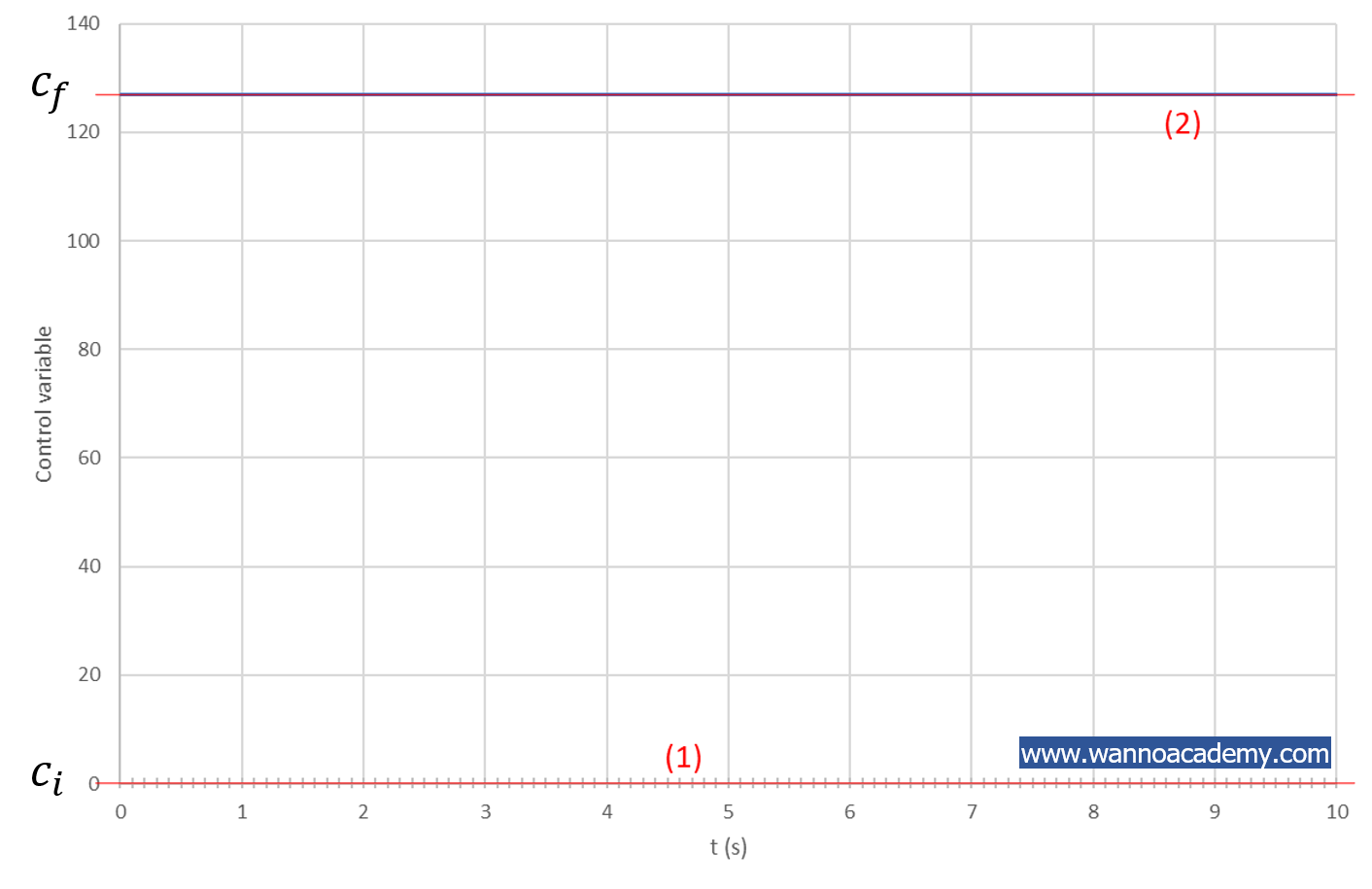
ในการลากเส้นตัดกราฟดังรูปที่ 5 โดยมีขั้นตอนต่างๆ ดังต่อไปนี้
*ลากเส้นตรง เส้น (1) ขนานกับแกน x และให้ตัดแกน y ที่ค่าเริ่มต้นของกราฟได้ตัวแปรคือ ![]()
*ลากเส้นตรง เส้น (2) ขนานกับแกน x และให้ตัดแกน y ที่ค่าสถานะอยู่ตัวของกราฟได้ตัวแปร ![]()
จากรูปที่ 5 จะได้ค่าต่างๆ ดังนี้
![]()
4 ทำการลากเส้นตัดกราฟเพื่อหาพารามิเตอร์ของเส้นโค้งปฏิกิริยาดังรูปที่ 6
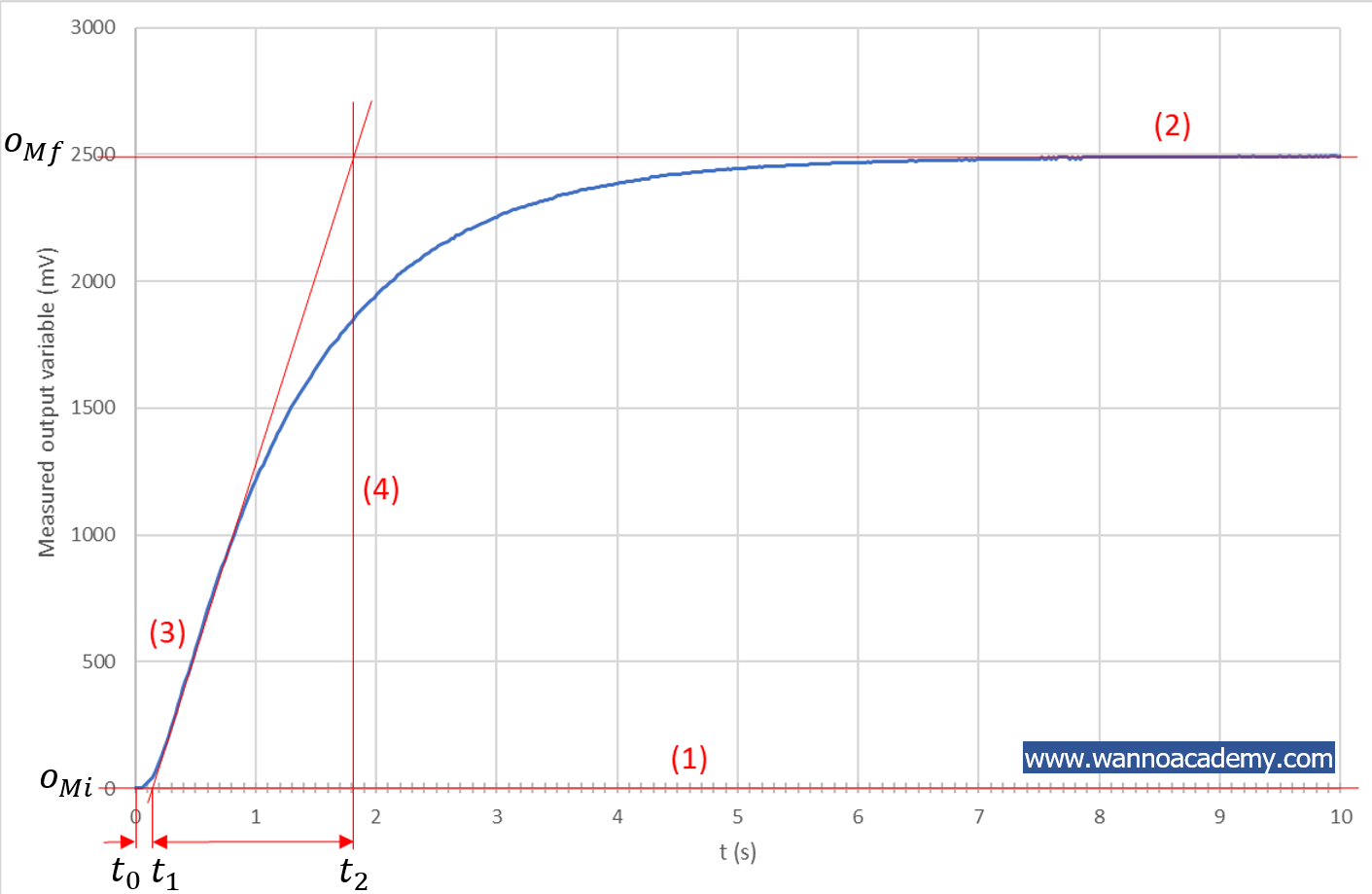
ในการลากเส้นตัดกราฟดังรูปที่ 6 โดยมีขั้นตอนต่างๆ ดังต่อไปนี้
*ลากเส้นตรง เส้น (1) ขนานกับแกน x และให้ตัดแกน y ที่ค่าเริ่มต้นของกราฟได้ตัวแปรคือ ![]() และเวลาที่จุดเริ่มต้นของกราฟคือ
และเวลาที่จุดเริ่มต้นของกราฟคือ ![]()
*ลากเส้นตรง เส้น (2) ขนานกับแกน x และให้ตัดแกน y ที่ค่าสถานะอยู่ตัวของกราฟได้ตัวแปร ![]()
*ลากเส้นตรง เส้น (3) สัมผัสกับจุดเปลี่ยนโค้งของกราฟ โดยลากเส้นยาวจนตัดกับเส้น (1) และ เส้น (2) โดยที่จุดตัดกับเส้น (1) ได้ตัวแปรคือ ![]()
*ลากเส้นตรง เส้น (4) ขนานแกน y และให้ตัดกับจุดที่เส้น (2) และเส้น (3) ตัดกัน โดยให้ลากลงมาตัดกับเส้น (1) ได้ตัวแปรคือ ![]()
5 นำค่าตัวแปรที่ได้จากกราฟอินพุตฟังก์ชันขั้นบันไดและจากเส้นโค้งปฏิกิริยามาใช้เพื่อหาพารามิเตอร์ที่ใช้ในการหาอัตราขยายของตัวควบคุม PID โดยกำหนดค่าต่างๆ ดังรูปที่ 7 ซึ่งค่าพารามิเตอร์ต่างๆ มีดังต่อไปนี้
![]() คือ เวลาประวิง
คือ เวลาประวิง
![]() คือ ค่าคงตัวทางเวลา
คือ ค่าคงตัวทางเวลา
![]() คือ อัตราขยายของระบบ
คือ อัตราขยายของระบบ
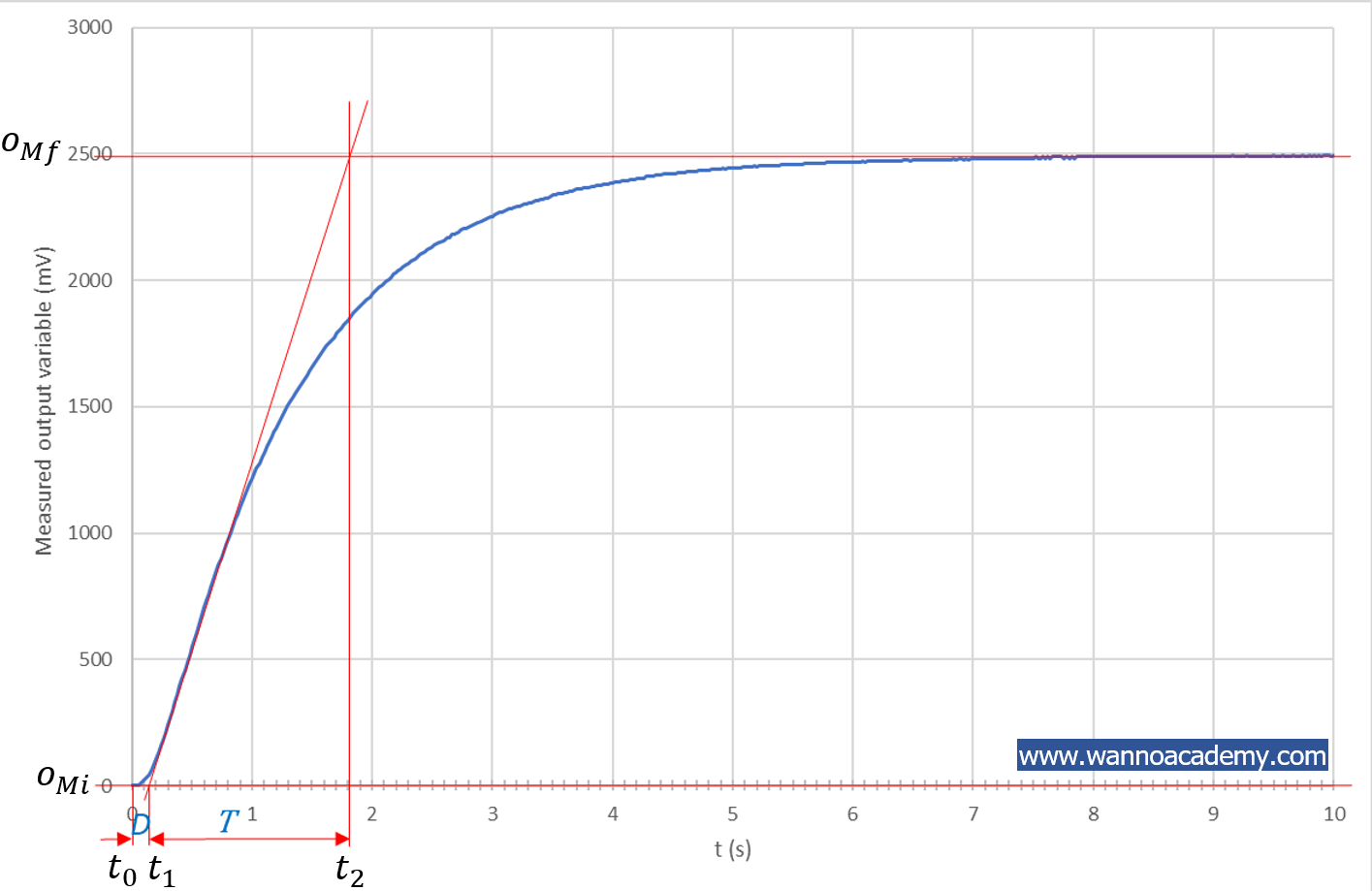
จากรูปที่ 7 จะได้ค่าต่างๆ ดังนี้
![]()
จากรูปที่ 6 และรูปที่ 7 สามารถหาพารามิเตอร์ต่างๆ ได้ดังต่อไปนี้
![]()
![]()
![]()
ดังนั้นจากรูปที่ 6 และ รูปที่ 7 จะได้ค่าพารามิเตอร์ต่างๆ ดังนี้
![]()
![]()
![]()
![]()
![]()
![]()
ดังนั้นสรุปได้ค่าพารามิเตอร์ของเส้นโค้งปฏิกิริยาเพื่อจะนำไปหาอัตราขยายตัวควบคุม PID ดังตารางที่ 1 คือ
ตารางที่ 1
| D | T | K |
| 0.14 | 1.67 | 19.62 |
เมื่อได้พารามิเตอร์ ![]() ,
, ![]() และ
และ ![]() จะนำพารามิเตอร์เหล่านี้ไปหาอัตราขยายตัวควบคุม PID ในบทความหน้าต่อไป
จะนำพารามิเตอร์เหล่านี้ไปหาอัตราขยายตัวควบคุม PID ในบทความหน้าต่อไป
ซึ่งบทความหน้าเป็นบทความที่หาอัตราขยายตัวควบคุม PID คือบทความ “Ziegler-Nichols vs Chien-Hrones-Reswick [ PID ]” ซี่งท่านสามารถคลิกที่ชื่อบทความเพื่อนำไปสู่บทความนี้ต่อไป
ข้อมูลเพิ่มเติม
- การควบคุมและเก็บข้อมูลการทดสอบได้ทำบนแพลตฟอร์มของ Arduino
- การนำข้อมูลซึ่งเป็นตัวเลขมาพล็อตเป็นกราฟใช้โปรแกรม Microsoft Excel
- เนื้อหาบางส่วน ของบทความฉบับนี้เป็นส่วนหนึ่งของ คอร์สตัวควบคุม PID ขั้นพื้นฐาน
หากท่านมีคำถามหรือข้อสงสัยประการใดสามารถสอบถามได้ที่
(เมื่อเข้า Wanno Acedemy ได้แล้ว กดส่งข้อความ เพื่อเริ่มพูดคุยกับผมได้เลยครับ)
